Humerus Analysis

Biologist Hermon Bumpus asserted that natural selection was present among species of the animal kingdom in 1899. As evidence, he presented findings from a recent study involving male House Sparrows. Following an abnormally severe winter storm, House Sparrows were collected and their humerus bones measured and documented for birds that both survived and perished in the storm.

My goal is to analyze the sampled data and evaluate the evidence supporting Bumpus' alternative hypothesis that the difference of sample mean wing sizes extends to the population and that such is evidence of natural selection at work in the animal kingdom.

Graphical Analysis

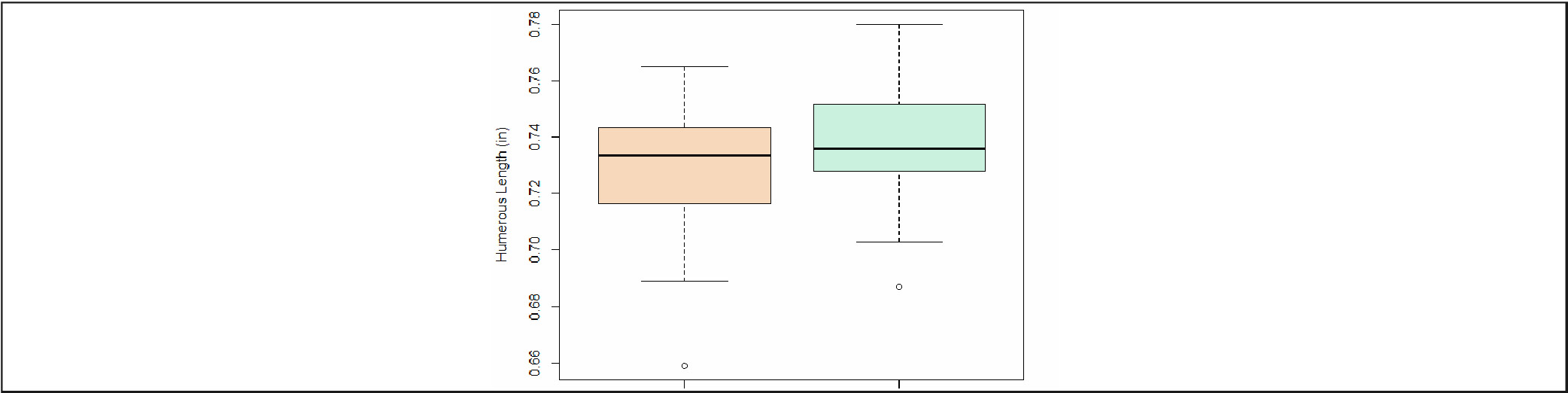
Analysis begins with a look into the distribution of our data, particularly between our two classifications: 'Survived' and 'Perished'. The below plot shows the distribution of each House Sparrow's humerus length by status following the storm.

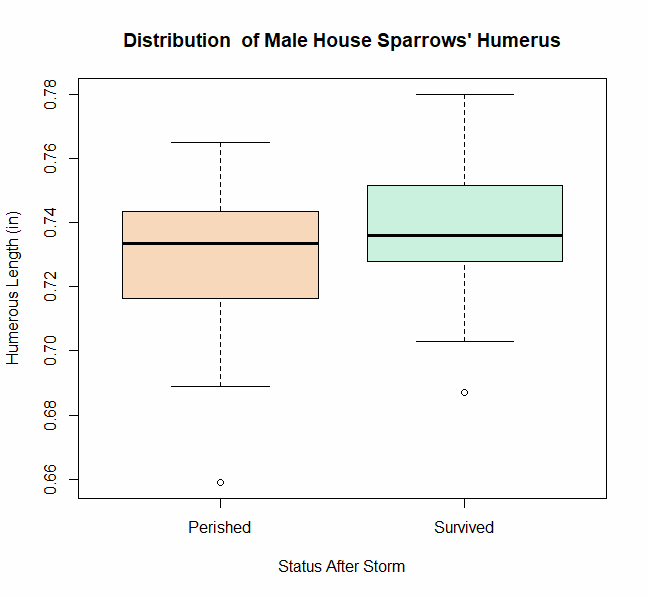
At first glance a lot seems to be similar between these distributions. The median values are nearly identical and the spread between the fences of each distribution is about the same. Each classification of fowl has an outlier on the lower end.

The one differences appear in the interquartile range, where we see the 'Perished' birds have a more left-skewed distribution while the 'Survived' birds are more right-skewed. Furthermore, the fences and 1st/3rd quartiles are noticeably longer for 'Survived' birds than for 'Perished'.

Statistical Analysis

What we're looking for now is for statistical evidence that these samples indicate a difference in humerus lengths for those that 'Survived' or 'Perished' from the storm (or said another way, a significantly low probability that our results happened by chance). I'll perform a student t test on this data, specifically evaluating the difference of our sample means. Below is the hypothesis test I'll conduct:

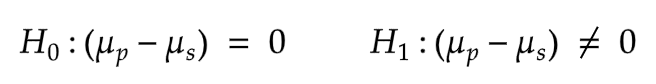
My null hypothesis is that humerus length between 'Perished' and 'Survived' House Swallows is zero, or that such a measurement had no relationship to their status following the storm, therefore rendering this study a poor example of natural selection. However, the alternative hypothesis will be Hermon Bumpus' assertion stated earlier: humerus length is not the same and natural selection in the animal kingdom contributed to the demise of smaller humerus Swallows.

As I declare in detail below (in the Assumptions section), I chose to use a two-sided t-test, with a significance level (α) of 0.05. The sample sizes from these two classifications are different, so I went with a non-paired test. I did, however, use an equal variance t-test as I'll explain further on. Our results were as follows:

Given the results of our t-test, we fail to reject the null hypothesis, concluding there to be insufficient evidence to support our null hypothesis of male House Sparrows' humerus lengths being different on average between 'Survived' and 'Perished' classifications in Bumpus' study. While the p-value is fairly low, it is higher than our stated level of significance. Furthermore, we can see from the confidence interval that 95% of the time our estimate for the true population difference of means includes zero.

Assumptions

While some, and certainly Hermon Bumpus, would interpret the above results more positively and thereby suggest to reject the null hypothesis, we have reason to suspect our assumptions aren't fully met (more on that below). While I chose to move forward with an analysis, I believed skepticism was warranted in how we evaluated our p-value.

The independence condition was met, as far as I could tell. The length of one sparrow's humerus isn't dependent on another, nor is there likely any reason to suspect that one sparrow 'Survived' because another 'Perished'. Equal variance was also met by my estimation. While the box plots had some mild, inversely skewed distributions, a Levene Test instilled confidence in equal variance between the two classifications (p-value of 0.5911).

I began to run into trouble with the normality of the two datasets. While we were certainly tipped off early with the box plots that this could be an issue, the Shapiro-Wilk test confirmed that, while the 'Perished' sample exhibits normality (p-value of 0.7624), the normality of 'Perished' sparrows was borderline non-normal (p-value of 0.095). I felt this was close enough for us to move forward with the analysis, but as stated above, meant we needed to be extra picky on our t-test p-value.

Furthermore, the assumption of random sampling was questionable. The description of the study lacked specifics about how the sparrow data was collected. Given the unknowns here, I felt compelled to proceed with the analysis but again take the results with a grain of salt.

Scope of Inference

The scope of inference here is pretty narrow by my estimation. Hermon Bumpus used these results to assert that natural selection is at play in the animal kingdom. Our results do not confirm this to be the case, but our type 2 error (β) does not rule it out. Therefore, I would not recommend using these findings, as Bumpus did, to argue on behalf of natural selection.

However, we can point out that due to the narrow scope of this study, other birds, types of natural forces, or other geographic regions are likely to produce different results. We cannot infer from our results that natural selection isn't at play elsewhere, only that we have insufficient evidence to claim it is working amongst locally sampled House Sparrows from an abnormally severe storm.